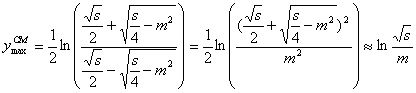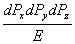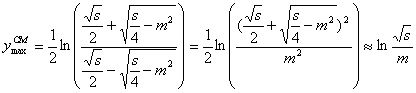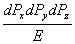擬ラピディティ

実験素粒子物理学において 擬ラピディティ（ぎラピディティ、英: pseudorapidity） η とは、粒子が粒子線軸となす角度を記述するために広く用いられる空間座標であり、次のように定義される。

${\displaystyle \eta \equiv -\ln \left[\tan \left({\frac {\theta }{2}}\right)\right]}$

ここで ${\displaystyle \theta }$ は粒子の三次元運動量 p と粒子線軸の正方向との成す角度である。逆に、以下の式も成り立つ。

${\displaystyle \theta =2\arctan \left(e^{-\eta }\right)}$

三次元運動量 p の関数として、擬ラピディティは以下のように書き下せる。

${\displaystyle \eta ={\frac {1}{2}}\ln \left({\frac {\left|{\boldsymbol {p}}\right| p_{\text{L}}}{\left|{\boldsymbol {p}}\right|-p_{\text{L}}}}\right)=\operatorname {artanh} \left({\frac {p_{L}}{\left|{\boldsymbol {p}}\right|}}\right)}$

ここで、 p_L は運動量の縦成分（英: longitudinal momentum、粒子線軸にそった成分）と呼ばれる。ハドロン衝突型加速器の分野では p_z と書くことも一般的である）である。粒子が光速に近い速さで運動する極限、または粒子の質量を無視する近似では${\displaystyle m\ll p\Rightarrow E\approx p\Rightarrow \eta \approx y}$ の置き換えが可能であり（つまり、この極限では粒子のエネルギーは光子と似て全てが運動エネルギーとなる）、したがって擬ラピディティは実験素粒子物理学で用いられるラピディティ

${\displaystyle y\equiv {\frac {1}{2}}\ln \left({\frac {E p_{\text{L}}}{E-p_{\text{L}}}}\right)}$

に収束する。

これは特殊相対論で定義されるラピディティとは、 |p| が p_L に置き換わる点で若干異なる。しかし、擬ラピディティは粒子の軌跡の極角にしか依存せず、エネルギーには依存しない。

ハドロン衝突型加速器の分野では、ラピディティ（および擬ラピディティ）は極角 θ よりも好んで用いられる。なぜならば、大雑把にいって、粒子の生成はラピディティの関数と見るとほぼ定数であり、そのためラピディティと擬ラピディティの「差」はローレンツ不変となるからである（速度がガリレイ変換について加法的であるのと同様に、ラピディティはローレンツ変換について加法的であるため）。一方、 θ の差はローレンツ不変ではない。このため、粒子の間の Δy および Δη は実験室系でもある粒子の静止系でも、基準系によらず一定となる。ハドロン衝突実験について、「前」方向というときそれは|η|の大きい、粒子線軸近くに設置される検知器の領域のことを指すが、「前」方向と「後」方向とを区別する場合、「前」は z 軸正方向、「後」は z 軸の負方向を表わす。

擬ラピディティの関数としてのラピディティは以下のように書き下せる。

${\displaystyle y=\ln \left({\frac {{\sqrt {m^{2} p_{T}^{2}\cosh ^{2}\eta }} p_{T}\sinh \eta }{\sqrt {m^{2} p_{T}^{2}}}}\right)}$

ここで ${\displaystyle p_{\text{T}}\equiv {\sqrt {p_{x}^{2} p_{y}^{2}}}}$ は運動量の横成分（英: transverse momentum、運動量の粒子線軸に垂直な成分）である。

擬ラピディティは粒子同士の進行方向の角度差を表すローレンツ不変な尺度を定義するために次のように用いることもできる。

${\displaystyle \left(\Delta R\right)^{2}\equiv \left(\Delta \eta \right)^{2} \left(\Delta \phi \right)^{2}}$

ここで、方位角の差 ${\displaystyle \Delta \phi }$ は粒子線軸（z 軸）に直交する面（x-y 平面）内で測られるため、粒子線軸にそった方向のローレンツブーストに対しては不変である。

値

代表的な値を以下に示す。

擬ラピディティは、 θ = 90° に対して奇関数である。すなわち、次の等式が成り立つ。

${\displaystyle \eta (\theta )=-\eta (180^{\circ }-\theta )}$

デカルト座標表示運動量への変換

ハドロン衝突型加速器により、運動量の横成分 p_T、横平面上の極角 ${\displaystyle \phi }$、そして擬ラピディティ η が測定できる。 デカルト座標表示した運動量 ${\displaystyle (p_{x},p_{y},p_{z})}$ （z軸は粒子線軸とする）を得るには、次のような変換式を用いる。

${\displaystyle p_{z}=p_{\text{T}}\sinh {\eta }}$

よって、

${\displaystyle |p|=p_{\text{T}}\cosh {\eta }}$

が成り立つ。

脚注