T分布型確率的近傍埋め込み法

t分布型確率的近傍埋め込み法（ティーぶんぷかくりつてききんぼううめこみほう、英語: t-distributed Stochastic Neighbor Embedding、略称: t-SNE）は、高次元データの個々のデータ点に2次元または3次元マップ中の位置を与えることによって可視化のための統計学的手法である。サム・ロウェイスとジェフリー・ヒントンにより最初に開発された確率的近傍埋め込み法を基にしており、ラウレンス・ファン・デル・マーテンがt分布版を提唱した。高次元データの可視化のため2次元または3次元の低次元空間へ埋め込みに最適な非線形次元削減手法である。具体的には、高次元のデータ集合を2次元または3次元へ配置する際に、高い確率で類似した集合が近傍に、異なる集合が遠方となるように対応付ける。

t-SNEのアルゴリズムは主に2つの段階で構成される。第一に、高次元データの各対について類似する集合が選択される可能性が高く、一方で異なる集合が選択される可能性が極めて小さくなるように確率分布を構築する。第二に、低次元マップ上の集合について同様な確率分布を定義し、2つの分布間のカルバック・ライブラー情報量を最小化する低次元マップ内の点の位置を求める。元のアルゴリズムは二点の類似度の指標にユークリッド距離を使用しているが、これは必要に応じ適切に変更する必要がある。

t-SNEは、コンピュータセキュリティ研究、音楽分析、癌研究,、バイオインフォマティクス、および生物医学信号処理を含む、幅広い応用の可視化に利用されている。人工ニューラルネットワークによって学習された高レベルの表現の可視化にもよく使用される。

多くの場合、t-SNEで表示された図ではクラスターが見えるが、可視化されたクラスターは選択したパラメータにより強く影響される可能性があるため、t-SNEのパラメータをよく理解することが必要である。そのような「クラスター」は、非クラスターのデータにも現れることがあり、したがって誤った発見かもしれない。したがって、パラメータを選択して結果を検証を繰り返す探索が必要となる可能性がある。t-SNEはよく分離されたクラスターを復元できることが多く、特別なパラメーターを選択により単純な形のスペクトルクラスター形状を近似することが実証されている。

詳細

高次元の${\displaystyle N}$個のデータ集合${\displaystyle \mathbf {x} _{1},\dots ,\mathbf {x} _{N}}$与えられているとする。高次元データ集合の類似度の特徴を反映した低次元上に表現された${\displaystyle N}$個のデータ集合${\displaystyle Y}$(${\displaystyle \mathbf {y} _{1},\dots ,\mathbf {y} _{N}}$) を求めるのが目的である。

t-SNEのパラメータとしてコスト関数のパラメータのパープレキシティ (perplexity) と最適化のパラメーターの反復計算回数${\displaystyle T}$、学習率${\displaystyle \eta }$、モーメンタム${\displaystyle \alpha (t)}$をそれぞれ与える。ファン・デル・マーテンによればt-SNEの性能は異なるパープレキシティの設定に対してはかなり頑健で、最適なパープレキシティは使用するデータにより異なるが典型的には5から50までの間の値が用いられる。

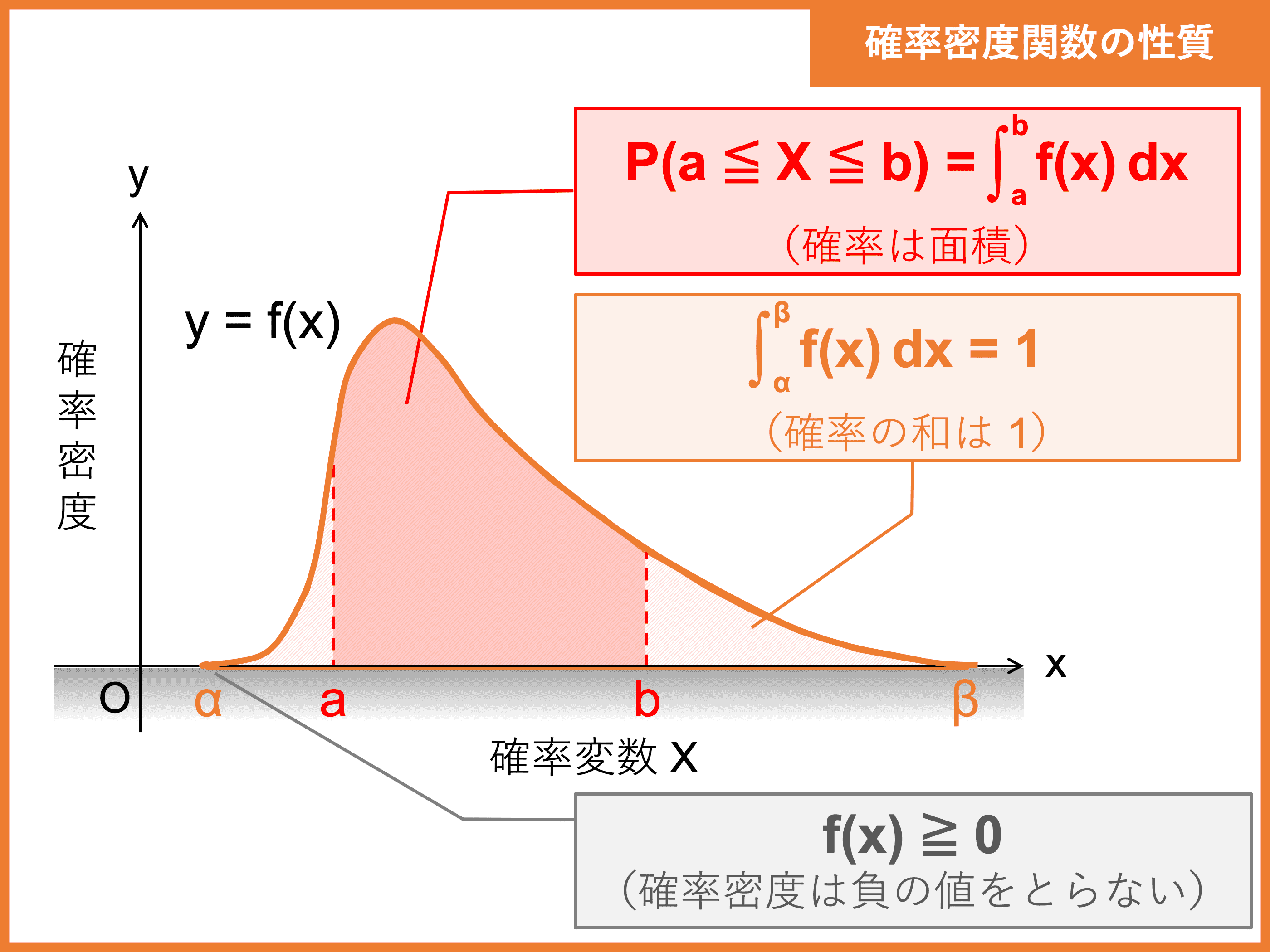
最初に高次元のデータ集合について各対の類似度を計算する。ファン・デル・マーテンとヒントンは「データ点${\displaystyle x_{i}}$に対してデータ点${\displaystyle x_{j}}$が${\displaystyle x_{i}}$を中心とするガウス分布の確率密度分布に比例して選ばれるならば、${\displaystyle x_{j}}$と${\displaystyle x_{i}}$の類似度は条件付き確率${\displaystyle p_{j|i}}$と表される」と説明した。

${\displaystyle p_{j\mid i}={\frac {\exp(-\lVert \mathbf {x} _{i}-\mathbf {x} _{j}\rVert ^{2}/2\sigma _{i}^{2})}{\sum _{k\neq i}\exp(-\lVert \mathbf {x} _{i}-\mathbf {x} _{k}\rVert ^{2}/2\sigma _{i}^{2})}},}$

ただし同じ点の対に対しては${\displaystyle p_{i\mid i}=0}$となる。

${\displaystyle \sigma _{i}}$はガウス分布の偏差で、次のパープレキシティの関係式を満たす偏差${\displaystyle \sigma _{i}}$を二分法により求める。

${\displaystyle Perp(P_{i})=2^{H(P_{i})}}$

${\displaystyle H(P_{i})=-\sum _{j}p_{j\mid i}\log _{2}p_{j\mid i}}$

ここで${\displaystyle H(P_{i})}$ はシャノンエントロピーである。密集していてデータ集合空間が小さければ${\displaystyle \sigma _{i}}$は小さい値となる。

次に同時確率${\displaystyle p_{ij}}$を次の式で求める。

${\displaystyle p_{ij}={\frac {p_{j\mid i} p_{i\mid j}}{2N}}}$

ただし${\displaystyle i=j}$ の場合は0となる。 ${\displaystyle p_{ii}=0}$

平均0のガウス分布の無作為標本を初期解${\displaystyle Y^{(0)}}$とする。

最後にt=1からt=Tまで以下の手順をT回の繰り返しにより解${\displaystyle Y^{(T)}}$を求める。

t-1番目の解${\displaystyle Y^{(t-1)}}$ に対する低次元上の類似度を計算する。

自由度1のt分布（コーシー分布）を利用した同時確率。

${\displaystyle q_{ij}={\frac {(1 \lVert \mathbf {y} _{i}-\mathbf {y} _{j}\rVert ^{2})^{-1}}{\sum _{k\neq l}(1 \lVert \mathbf {y} _{k}-\mathbf {y} _{l}\rVert ^{2})^{-1}}}}$

ただし同じ点の対に対しては0とする。${\displaystyle q_{ii}=0}$

${\displaystyle p_{ij}}$の分布Pと${\displaystyle q_{ij}}$の分布Qについてのカルバック・ライブラー情報量を目的関数とし、最小となる解${\displaystyle Y^{(t)}}$求める。

${\displaystyle KL(P||Q)=\sum _{i\neq j}p_{ij}\log {\frac {p_{ij}}{q_{ij}}}}$

各iについて目的関数の勾配を計算する。

${\displaystyle {\frac {\delta C}{\delta y_{i}}}=4\sum _{j}(p_{ij}-q_{ij})(y_{i}-y_{j})(1 \lVert y_{i}-y_{j}\rVert ^{2})^{-1}}$

目的関数の勾配と以前の解よりt番目の解${\displaystyle Y^{(t)}}$を計算する。

${\displaystyle Y^{(t)}=Y^{(t-1)} \eta {\frac {\delta C}{\delta Y}} \alpha (t)\left(Y^{(t-1)}-Y^{(t-2)}\right)}$

解${\displaystyle Y^{(T)}}$を図示することで高次元のデータ集合のクラスターを把握できる。

弱点

• 一般的な次元削減課題をどのように実行するかが不明確である。
• 比較的局所的な性質によりデータの固有次元の呪いに敏感になる。
  • ガウス関数はユークリッド距離 ${\displaystyle \lVert x_{i}-x_{j}\rVert }$を使用しているため、次元の呪いの影響を受け、高次元でデータを距離により区別する能力が失われる。${\displaystyle p_{ij}}$はほとんど同じ値となる（高次元で定数に漸近する）。これを軽減するために、各点の固有の次元に基づいて、冪乗変換により距離を調節する手法が提案されている。
• t目的関数の大域的最小値への収束が保証されていない。
  • 同じアルゴリズムパラメータでも得られる解が異なることがある。

脚注

外部リンク

• https://lvdmaaten.github.io/tsne/ ラウレンス・ファン・デル・マーテンによるt分布型確率的近傍埋め込み法の解説
• Visualizing Data Using t-SNE, t-SNEに関するGoogle Tech Talk