計算化学において、ポスト-ハートリー-フォック法(ポスト-ハートリー-フォックほう、英: Post–Hartree–Fock methods)は、ハートリー–フォック法(平均場近似)を改善するために開発された一連の手法である。ポスト-ハートリー-フォック法によって電子相関エネルギーが加えられる。何れも波動関数として複数のスレイター行列式の線形結合をとったものを使っており、計算精度を上げるに従って計算コストは飛躍的に増大する。
詳細
一般に、自己無撞着場(SCF)手順は多体シュレーディンガー方程式とその解の集合の性質に関していくつかの仮定を行う。
- 分子では、ボルン–オッペンハイマー近似が本質的に仮定される。真の波動関数はそれぞれの核の座標の関数でもあるべきである。
- 典型的には、相対論的効果は完全に無視される。運動量演算子は完全に非相対論的であると仮定される。
- 基底関数系は有限の数の直交関数から構成される。真の波動関数は完全(無限)基底関数系からの関数の線形結合である。
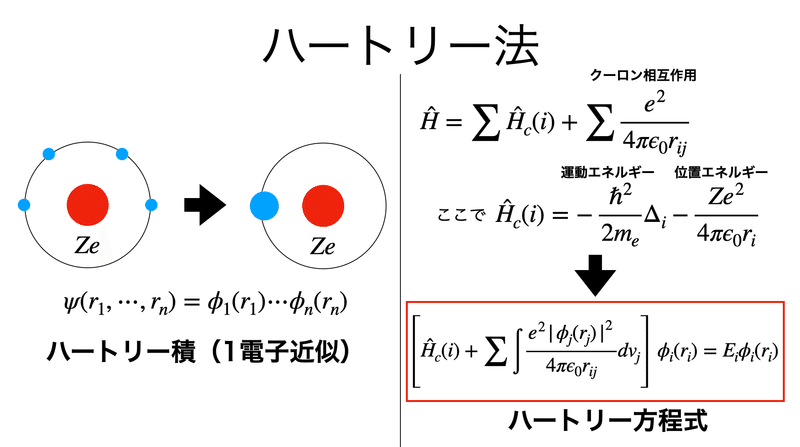
- エネルギー固有関数は1電子波動関数の積であると仮定される。波動関数の反対称化から生じる交換エネルギーの効果を超える電子相関の効果は完全に無視される。
研究される大多数の系、特に励起状態や分子解離反応といった過程について、4項目目が間違いなく最も重要である。結果として、「ポスト-ハートリー-フォック法」という用語は典型的に系の電子相関を近似する手法に対して用いられる。
大抵、ポスト-ハートリー-フォック法はハートリー-フォック計算よりも正確な結果を与えるが、精度の向上には計算コストの増大という代償が伴う。
ポスト-ハートリー-フォック法
- 配置間相互作用(CI)
- 結合クラスター法(CC)
- 多配置時間依存ハートリー(MCTDH)
- メラー–プレセット摂動理論(MP2、MP3、MP4等)
- 2次的配置間相互作用(QCI)
- 量子化学複合手法(G2、G3、CBS、T1等)
関連手法
2つ以上の行列式を使用する手法は厳密にはポスト-ハートリー-フォック法(参照として単一の行列式を使用する)ではないが、これらの手法は電子相関の記述を改善するためにしばしば同様の摂動法や配置間相互作用法を用いる。
- 多配置自己無撞着場 (MCSCF)
- 多参照1,2電子励起配置間相互作用法 (MRCISD)
- n電子原子価状態摂動理論 (NEVPT)
出典
推薦文献
- Jensen, F. (1999). Introduction to Computational Chemistry. New York: John Wiley & Sons. ISBN 0471980854
関連項目
- 完全活性空間摂動理論(CASPTn)